Category: C/C++

Binary search tree is a binary tree in which each internal node x stores an element such that the elements stored in the left subtree of x are less than or equal to x and elements stored in the right subtree are greater than or equal to x. The following code is the class of binary search tree designed by me. I use a function pointer m_visit to construct the tree and visit the nodes of the tree.

template<typename T>
class BSTreeNode
{
public:
    BSTreeNode(T d, BSTreeNode<T> *p=NULL, BSTreeNode<T> *l=NULL,
               BSTreeNode<T> *r=NULL):data(d),parent(p),left(l),right(r){}
    T data;
    BSTreeNode<T> *parent;
    BSTreeNode<T> *left;
    BSTreeNode<T> *right;
};

template<typename T>
class BSTree
{
protected:
    BSTreeNode<T> *m_root;

// A function pointer that points the visit function
    typedef void (*v_func)(const T &data);
    v_func m_visit;//the visit function pointer
    void Inorder(BSTreeNode<T> *);//Inorder traversal of the tree
public:
    BSTree(v_func f, BSTreeNode<T> *p=NULL): m_visit(f), m_root(p) {}
    BSTreeNode<T>* GetRoot() { return m_root; } const

//inorder tree walk, thus prints a sorted list
    void InorderWalk() { Inorder(m_root);}
//query on the binary search tree
    BSTreeNode<T>* Search(const T &);
//find the successor of the given node in the sorted order which
//is determined by an inorder tree walk
    BSTreeNode<T>* Successor(BSTreeNode<T>*);
//return the maximum element of the binary tree
    const T& Maximum(void);
//return the minimum element of the binary tree
    const T& Minimum(void);
//insert a new value into the binary search tree
    void Insert(const T&);
//insert a new value with recursive version procedure
    void Insert2(const T&, BSTreeNode<T>*);
//delete a node from the binary search tree
    BSTreeNode<T>* Delete(BSTreeNode<T>*);
};

Let’s walk through the procedure of searching a given key in the above binary search data structure.

The procedure begins its search at the root and traces a path downward in the tree, and for each node it encounters, it compares the keys. If the searched key is bigger than the current key of the node, it goes down to left subtree. If the searched key is smaller than the current key of the node, it goes down to right subtree. If two keys are equal, the search terminates.

template<typename T>
BSTreeNode<T>* BSTree<T>::Search(const T &d)
{
    BSTreeNode<T>* p = m_root;
    while(p && p->data!=d)
    {
        if(p->data > d)
            p=p->left;
        else
            p=p->right;
    }
    return p;
}

The structure of a binary search tree allows us to determine the In Order successor of a node without ever comparing keys. The following procedure returns the successor of a node x in a binary search tree if it exists, or NULL if x has the largest key in the tree.

template<typename T>
BSTreeNode<T>* BSTree<T>::Successor(BSTreeNode<T>* x)
{
    //return the node x's successor if it exists.
    if(!x)
        return NULL;
    BSTreeNode<T>* y=x->right;

    //if x has right children, just return the leftmost node
    //in the right subtree.
    if(y)
    {
        while(y->left)
            y=y->left;
        return y;
    }


    //if x has no right child, then x's successor is the lowest
    //ancestor of x
    else
    {   //whose left child is also an ancestor of x.
        y=x->parent;
        while(y && x!=y->left)
        {
            x=y;
            y=y->parent;
        }
        return y;
    }
}

An element in a binary search tree whose key is a minimum can always be found by following left child pointers from the root until a NULL is encountered, thus the procedure of finding the maximum element is symmetric.

template<typename T>
const T& BSTree<T>::Minimum()
{
    BSTreeNode<T>* p = m_root;
    while(p->left)
        p=p->left;
    return p->data;
}
template<typename T>
const T& BSTree<T>::Maximum()
{
    BSTreeNode<T>* p = m_root;
    while(p->right)
        p=p->right;
    return p->data;
}

To insert a node into a binary search tree, we use a node pointer x which begins at the root of the tree and traces a path downward. The pointer x traces the path, and the pointer y is maintained as the parent of x. These two pointers to move down the tree, going left or right depending on the comparison of the key to be inserted with x->data, until x is set to NULL. At that time, we use y to help us to insert the key. Insert2 is a recursive version of the insertion procedure.

template<typename T>
void BSTree<T>::Insert(const T& da)
{
    BSTreeNode<T>* x=m_root,*y=NULL;
    if(!x)//the tree is empty
        m_root = new BSTreeNode<T>(da);
    else
    {
        while(x)
        {
            y=x;//store x's parent;
            if(da > x->data)
                x=x->right;
            else
                x=x->left;
        }//now y is the insertion node's parent
        x = new BSTreeNode<T>(da);
        x->parent=y;
        if(da > y->data)
            y->right=x;
        else
            y->left=x;
    }
}

template<typename T>
void BSTree<T>::Insert2(const T& data, BSTreeNode<T>* z=NULL)
{
    BSTreeNode<T>* x;
    if(!z)
    {
        m_root = new BSTreeNode<T>(data);
        return;
    }
    if(data > z->data && z->right)
        Insert2(data,z->right);
    if(data <= z->data && z->left)
        Insert2(data,z->left);

    if(!z->right && data > z->data)
    {
        x = new BSTreeNode<T>(data);
        z->right = x;
        x->parent = z;
    }

    if(!z->left && data < z->data)
    {
        x = new BSTreeNode<T>(data);
        z->left = x;
        x->parent = z;
    }
}

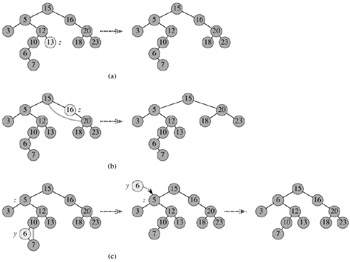
However, removing a node from a binary search tree is a bit more complex. Which node is actually removed is depends on how many children the node to be deleted has. If the node has one child then the child is spliced to the parent of the node, which means that we should remove the node itself. If the node has two children then its successor has no left child; copy the successor into the node and delete the successor instead. The following figure shows deleting a node z from a binary search tree. (a) z has no children, we just remove it. (b) z has only one child, we splice out z. (c) z has two children, we splice out its successor y, which has at most one child, and then replace z’s key and data with y’s key and data.

 

template<typename T>
void BSTree<T>::Delete(BSTreeNode<T>* z)
{
    if(!z)
        return NULL;
//y is the node should be removed, and x is the child of y
    BSTreeNode<T> *y, *x;
//if z has 2 children, we should remove its successor
    if(z->left && z->right)
        y=Successor(z);
    else//if z has 1 or no child, z itself should be removed.
        y=z;

//Let x be the y's child and if y is the successor of z,
//notice that x has at most one child
    if(y->left)
        x=y->left;
    else
        x=y->right;

//begin to remove y from the tree
    if(x)
        x->parent=y->parent;
    if(!y->parent)//if y is the root, let x be the root
        m_root=x;
    else
    {
        if(y==y->parent->left)
            y->parent->left = x;
        else
            y->parent->right = x;
    }

//if z has 2 children and we split out its successor
    if(y!=z)
        z->data=y->data;
    delete y;
}

Finally, Here is the piece of code to test out my little binary search tree. The function print() visits the data of the tree node. The rand() function can generate random integers ranges from -999 to 999 approximately.

#include <iostream>
#include <time.h>
time_t* tp;
int randx =time(tp);
int rand()
{
    randx = randx * 12345;
    return randx % 1000;
}
static void print(const int& data)
{
    cout<<data<<" ";
}

int main()
{
    BSTree<int> bstree1(&print);
    int i;
    for(i=0;i<10;i++)
        bstree1. Insertion(rand(),bstree1.GetRoot());
    bstree1.InorderWalk();
    cout<<endl;
    int min=bstree1.Minimum();
    int max=bstree1.Maximum();
    cout<<"The minimum element is: "<<min<<endl;
    cout<<"The maximum element is: "<<max<<endl; int secondmin=bstree1.Successor(bstree1.Search(min))->data;
    cout<<"The second minimum element is : "<<secondmin<<endl;
    int del=1;
    while(del!=0){
        cout<<"Choose an item to be deleted(Input '0' to quit):"; cin>>del;
        if(bstree1.Delete(bstree1.Search(del)))
            cout<<"Deletion Completed!n";
        bstree1.InorderWalk();
        cout<<endl;
    }
    return 0;
}